Guida Completa alla Regressione Lineare su Excel
Indice
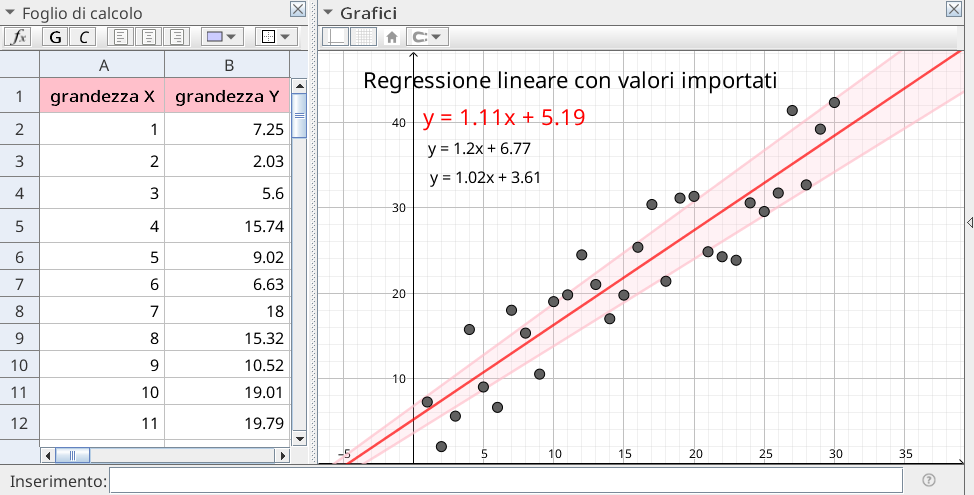
La regressione lineare è uno strumento statistico fondamentale per l’analisi dei dati, ampiamente utilizzato in vari settori per prevedere un’uscita (variabile dipendente) basandosi su un insieme di variabili indipendenti. Excel, il popolare software di foglio di calcolo di Microsoft, offre potenti strumenti per eseguire analisi di regressione lineare, rendendo questo processo accessibile anche a chi non possiede una profonda conoscenza statistica.
Attraverso l’utilizzo del metodo dei minimi quadrati, Excel è in grado di calcolare la retta di regressione che meglio si adatta al set di dati fornito, fornendo così una base solida per le previsioni e l’interpretazione delle relazioni tra le variabili.
Questa guida intende illustrare come sfruttare al meglio le capacità di Excel nella regressione lineare, spiegando passo dopo passo come eseguire questa analisi e interpretarne i risultati.
Che si tratti dell’analisi della relazione tra spesa pubblicitaria e vendite, o dello studio dell’impatto delle condizioni meteorologiche sulla produzione agricola, la comprensione della regressione lineare attraverso Excel apre nuove prospettive nell’analisi dei dati.
Introduzione alla Regressione Lineare con Excel e suo Utilizzo
La regressione lineare rappresenta un pilastro fondamentale nell’ambito delle tecniche statistiche, indispensabile per esplorare le interazioni tra due variabili quantitative. Questo metodo consente di predire il valore di una variabile, definita dipendente, basandosi su un’altra, detta indipendente, attraverso l’identificazione di una retta di regressione. Quest’ultima rappresenta la migliore approssimazione dei dati su un piano cartesiano, illustrando la relazione diretta tra le variabili in questione.
L’adozione della regressione lineare attraverso Excel facilita enormemente tale processo, grazie ai suoi avanzati strumenti di analisi di regressione e all’implementazione del metodo dei minimi quadrati. Queste funzionalità trasformano Excel da semplice programma per la gestione dei fogli di calcolo a uno strumento avanzato per l’analisi predittiva e statistica. In pochi passaggi, è possibile condurre analisi dettagliate, visualizzare i risultati mediante grafici intuitivi e interpretare senza ostacoli le principali metriche di regressione, come il coefficiente di determinazione (R²). Questo indicatore quantifica l’adattamento dei dati alla retta di regressione, offrendo una misura dell’accuratezza della previsione.
Apprendere l’utilizzo della regressione lineare in Excel non solo apre la porta a nuove possibilità nell’ambito dell’analisi dei dati ma si rivela essenziale in una vasta gamma di applicazioni, dalle previsioni finanziarie alle indagini scientifiche. Imparare a navigare tra le variabili e a dedurre le loro relazioni svela nuovi orizzonti analitici, rendendo Excel uno strumento potente e versatile per ogni professionista dei dati.
 Passo dopo Passo: Eseguire una Regressione Lineare Utilizzando Excel
Passo dopo Passo: Eseguire una Regressione Lineare Utilizzando Excel
1. Inserimento dei dati:
- Disporre i dati delle variabili indipendenti (X) e dipendenti (Y) in due colonne separate all’interno di un foglio di lavoro Excel.
- Assicurarsi che i dati siano formattati correttamente come numeri.
2. Attivazione dell’analisi dei dati:
- Cliccare sul tab “Dati”.
- Se l’opzione “Analisi dei dati” non è presente, attivare il componente aggiuntivo “Strumenti per l’analisi” tramite:
- File > Opzioni > Componenti aggiuntivi
- Selezionare “Strumenti per l’analisi” e cliccare su “Vai”
- Spuntare la casella “Strumenti per l’analisi” e cliccare su “OK”
3. Esecuzione della regressione lineare:
- Cliccare su “Analisi dei dati” nel tab “Dati”.
- Selezionare “Regressione” dall’elenco delle analisi disponibili.
- Nella finestra di dialogo “Regressione”:
- Specificare l’intervallo di celle che contiene i dati per la variabile indipendente (X) nella casella “X”.
- Specificare l’intervallo di celle che contiene i dati per la variabile dipendente (Y) nella casella “Y”.
- Scegliere se includere o meno i titoli delle colonne nell’analisi (opzionale).
- Selezionare la posizione in cui visualizzare l’output dell’analisi: “Nuovo foglio di lavoro” o “Foglio di lavoro corrente”.
- Cliccare su “OK” per avviare l’analisi.
4. Interpretazione dell’output:
L’output della regressione lineare in Excel include diverse informazioni:
- Coefficienti di regressione: Indicano l’impatto di ciascuna variabile indipendente sul valore previsto della variabile dipendente.
- Coefficiente R²: Indica quanto bene la retta di regressione si adatta ai dati. Un valore di R² vicino a 1 indica una forte correlazione tra le variabili.
- Errore standard di stima: Indica la media degli errori tra i valori reali e quelli previsti dalla retta di regressione.
- Test di significatività: Valuta la significatività statistica dei coefficienti di regressione.
5. Conclusioni:
- Analizzare i coefficienti di regressione e il coefficiente R² per trarre conclusioni sull’influenza delle variabili indipendenti nella previsione del valore della variabile dipendente.
- Considerare l’errore standard di stima e i test di significatività per valutare l’affidabilità dei risultati.
Esempio:
Supponiamo di avere dati sulla superficie di una casa (variabile indipendente) e sul suo prezzo di vendita (variabile dipendente). Utilizzando la regressione lineare in Excel, possiamo determinare la relazione tra queste due variabili e stimare il prezzo di vendita di una casa con una data superficie.
Suggerimenti:
- Per una migliore visualizzazione della relazione tra le variabili, creare un grafico a dispersione con la retta di regressione sovrapposta.
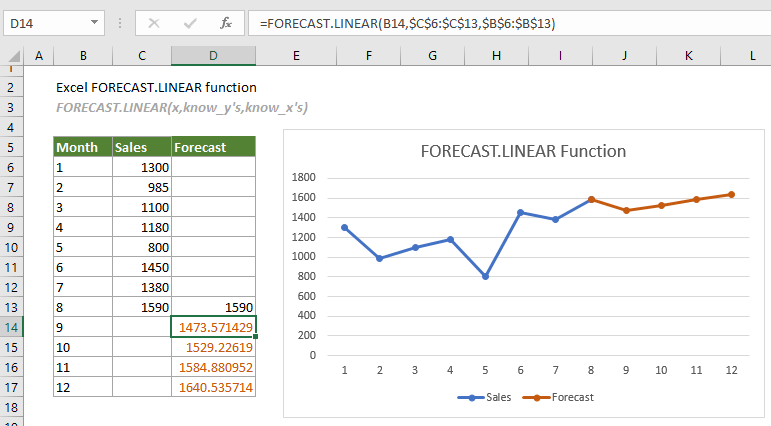
- È possibile utilizzare la funzione REGR.LIN di Excel per ottenere i coefficienti di regressione e altre informazioni statistiche senza dover utilizzare l’analisi dei dati.
 Interpretazione dei Risultati della Regressione Lineare Excel
Interpretazione dei Risultati della Regressione Lineare Excel
Capito il verdetto della regressione lineare?
Fantastico! Ora viene il bello: dare un senso a tutti quei numeri.
Cosa significa R^2?
Immagina R^2 come un misuratore di quanto bene la tua linea di regressione si adatta ai dati. Più è vicino a 1 (tipo 0,9 o 0,8), più la linea “calza” a pennello. Ma attenzione: un R^2 alto non significa per forza che c’è una vera e propria relazione di causa-effetto tra le variabili!
I coefficienti della retta di regressione: pendenza e intercetta
- Pendenza: quanto la variabile dipendente “sale” o “scende” in media per ogni unità di cambiamento della variabile indipendente. In parole povere, se la superficie di una casa aumenta di un metro quadrato, quanto aumenta il prezzo di vendita?
- Intercetta: il valore della variabile dipendente quando la variabile indipendente è zero (un po’ come l’origine del grafico).
Ma sono affidabili questi coefficienti?
Ecco che entra in gioco la significatività statistica. Se il valore p è inferiore a 0,05, significa che c’è una buona probabilità che la relazione tra le variabili non sia casuale.
E gli intervalli di confidenza?
Ci aiutano a capire la precisione delle stime dei coefficienti. Più l’intervallo è stretto, più la stima è precisa.
Ok, numeri alla mano, che cosa facciamo?
Ecco il punto chiave: tradurre i dati in azioni concrete o in spunti per future analisi o decisioni aziendali. Ma attenzione: per farlo serve sia una solida base di statistica che una conoscenza approfondita del contesto in cui si sta lavorando.
In parole semplici:
- La regressione lineare ci fornisce una serie di informazioni utili per capire la relazione tra due variabili.
- È importante interpretare i risultati con attenzione e non limitarsi a una mera analisi numerica.
- Solo contestualizzando i dati e usando il buon senso è possibile trarre conclusioni affidabili e utilizzarle per prendere decisioni informate.
Spero che questa spiegazione sia stata il più comprensibile possibile e possa presto tornarti utile!